零知识证明技术应用广泛,如隐私证明、计算证明、共识证明等。在寻找更多更好的应用场景的同时,很多人逐渐发现零知识证明性能是一个瓶颈。Trapdoor Tech团队从2019年开始深入研究零知识证明技术,一直在探索高效的零知识证明加速方案。GPU或FPGA是目前市面上常见的加速平台。从M的计算入手,分析了FPGA和GPU加速零知识证明计算的优缺点。
ZKP是一项未来前景广阔的技术。越来越多的应用开始采用零知识证明技术。然而,有许多ZKP算法,不同的ZKP算法用于不同的项目。同时,ZKP证明的计算性能较差。本文详细分析了M算法、椭圆曲线点加法算法和蒙哥马利乘法算法,比较了BLS12_381曲线点加法中GPU和FPGA的性能差异。一般来说,在ZKP证明计算中,短期GPU具有明显的优势,如高吞吐量、高性价比、可编程性等。相对来说,FPGA在功耗上有一定的优势。从长远来看,可能会有适合ZKP计算的FPGA芯片,或者为ZKP定制的ASIC芯片。
ZKP算法复杂ZKP是零知识证明技术的统称。主要有两种分类:zk蛇和ZK蛇。目前zk-SNARK常用的算法有Groth16、PLONK、PLOOKUP、Marlin和Halo/Halo2。zk-SNARK算法的迭代主要沿着两个方向:1/是否需要可信设置的性能2/电路结构?zk-STARK算法的优点是不需要可信设置,但是验证了计算量是对数线性的。
就zk-SNARK/zk-STARK算法的应用而言,不同项目使用的零知识证明算法相对分散。在zk-SNARK算法的应用中,由于PLONK/Halo2算法具有普适性(不需要可信设置),所以使用的可能会越来越多。
PLONK证明计算以PLONK算法为例分析PLONK证明的计算。
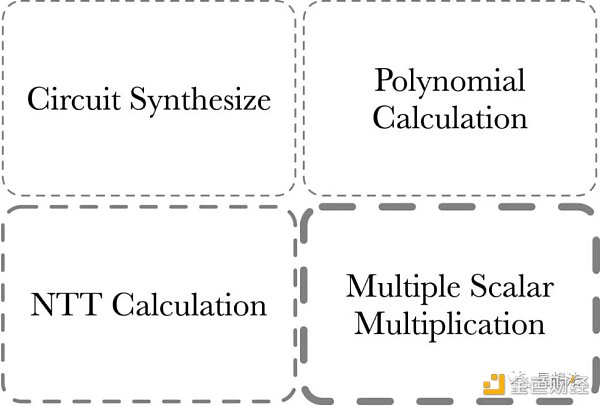
PLONK证明部分的计算由四部分组成:
1/M & # 8211;多重标量乘法.m通常用于计算多项式承诺。
2/ NTT计算& # 8211;点值和系数表示之间的多项式变换。
3/多项式计算& # 8211;多项式加减乘除。多项式求值等等。
4/电路合成器& # 8211;电路综合。这部分计算与电路的规模/复杂度有关。
一般来说,电路综合部分的计算量更多的是判断和循环逻辑,并行性更低,更适合CPU计算。一般来说,零知识证明加速一般是指前三部分的计算加速。其中,M的计算量相对最大,其次是NTT。
什么& # 8217;Smm(多标量乘)是指给定椭圆曲线上的一系列点和标量,计算点相加结果对应的点。
例如,给定椭圆曲线上的一系列点:
给定来自一条指定曲线的一组固定椭圆曲线点:
皮彭格算法的计算过程分为两步:
1/标量分为窗口。如果标量是256位,窗口是8位,那么所有标量分区都是256/8=32个窗口。在每一层的窗口中,一个“桶”用来临时存储中间结果。GW_x是第一层累积结果的点。计算GW_x也比较简单,依次遍历一层中的每个标量,按照标量层的值作为索引,将对应的G_x加到对应的桶中。其实原理比较简单。如果两个点的系数相同,则先将两个点相加,然后再将标量相加,而不是将两个点相加两次再累加。
2/每个窗口计算出来的分数用双加累加,得出最终结果。
Pippenger算法也有很多变形优化算法。无论如何,M算法的底层计算都是椭圆曲线上的点加法。不同的优化算法对应不同的点数。
椭圆曲线上的点加你可以从这个网站上以“简短Weierstrass”的形式看椭圆曲线上的点加的各种算法。
http://www . hyperellipic . org/EFD/g1p/auto-short w-Jacobian-0 . html # addition-madd-2007-bl
假设两点的射影坐标分别为(x1,y1,z1)和(x2,y2,z2),点相加的结果(x3,y3,z3)可以通过下面的计算公式计算出来。

之所以详细给出计算过程,是为了说明整个计算过程多为整数运算。整数的位宽取决于椭圆曲线的参数。给出了一些常见椭圆曲线的位宽:
BN256 & # 8211256位
BLS12 _ 381 & # 8211381位
BLS12 _ 377 & # 8211377位
特别需要注意的是,这些整数运算都是模块域上的运算。模加减比较简单,重点讲模乘的原理和实现。
模乘给出一个模域中的两个值:x和y,模乘计算参考x * y mod p,注意这些整数的位宽是椭圆曲线的位宽。模乘的经典算法是模乘。在蒙哥马利乘法之前,需要将被乘数转换成蒙哥马利表达式:
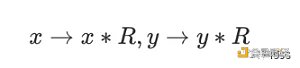
蒙哥马利乘法的计算公式如下:
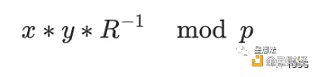
Montgomery乘法算法有很多:CIOS(粗集成运算器和扫描),FIOS(精集成运算器和扫描),FIPS(精集成积扫描)等等。本文不深入介绍各种算法的实现细节,有兴趣的读者可以自行研究。
为了比较FPGA和GPU的性能差异,选取了最基本的算法实现方式:
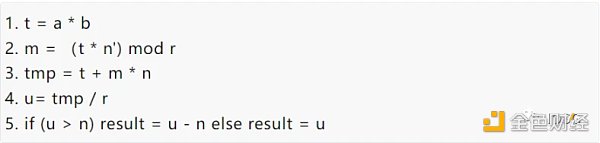
简单来说,模乘算法可以进一步分为大数乘法和大数加法两种计算。在理解M的计算逻辑的基础上,我们可以选择吞吐量来比较FPGA和GPU的性能。
在这样的FPGA设计下观察和思考,我们可以估算出BLS12_381椭圆曲线点加上吞吐量,整个VU9P能提供什么。点加法(add_mix模式)需要大约12次模乘。FPGA的系统时钟为450M。

在相同的模乘/模加算法和相同的点加算法下,Nvidia 3090的点加吞吐率(考虑数据传输因素)超过500 m/s,当然整个计算涉及多种算法,有些可能适合FPGA,有些适合GPU。我想比较一下FPGA和GPU的核心计算能力,原因是一样的。
基于以上结果,总结GPU和FPGA的ZKP证明性能比较:
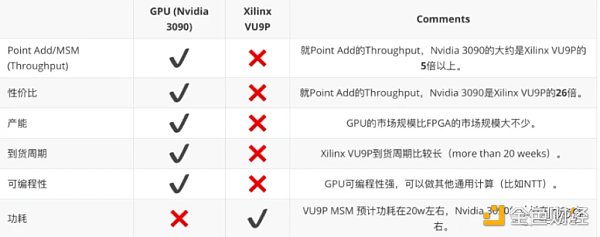
总结越来越多的应用开始采用零知识证明技术。然而,有许多ZKP算法,不同的ZKP算法用于不同的项目。从我们的实际工程经验来看,FPGA是一个选项,但目前GPU是一个性价比较高的选项。FPGA更倾向于确定性计算,确定性计算具有延迟和功耗方面的优势。GPU可编程性强,有相对成熟的高性能计算框架,开发迭代周期短,偏好吞吐量场景。
温馨提示:注:内容来源均采集于互联网,不要轻信任何,后果自负,本站不承担任何责任。若本站收录的信息无意侵犯了贵司版权,请给我们来信,我们会及时处理和回复。
原文地址"fpga加速卡干嘛用的,fpga 硬件加速":http://www.ljycsb.cn/qukuailian/215287.html。

微信扫描二维码投放广告
▲长按图片识别二维码


